
今回は前回のRadix-2 Decimation-In-Time FFTで得られた振幅の解釈に関して解説していきます。
Radix-2 Decimation-In-Time (DIT) FFTで周波数解析を行った場合、得られるN個の複素数出力(振幅と位相)は、Fsをサンプリング周波数とすると0Hzからナイキスト周波数(Fs/2)までの周波数成分と、それ以上の周波数成分のエイリアシング、または負の周波数成分を含んでいます。
一般的にN個(偶数)のサンプルからRadix-2 Decimation-In-Time (DIT) FFTを行った場合、N個の要素が出力されます。その要素はインデックスk=0からk=Nまで順番に出力されますが、それぞれの要素は以下の意味を持ちます。
・インデックスk=0(FFT出力の最初の要素):0Hz (直流成分):に対応します。
・インデックスk=1からk=N/2-1:それぞれの周波数はk・Fs/N に対応します。
・インデックスk=N/2:ナイキスト周波数(Fs/2)に対応します。この成分は、サンプリング周波数の半分であり、折り返し雑音(エイリアシング)が発生する境界周波数です。
・インデックスk=N/2+1からk=N-1:負の周波数成分、またはナイキスト周波数を超えて折り返された(エイリアシングによって低周波数帯に現れた)正の周波数成分に対応します。
これらの成分は、通常はスペクトルをプロットする際には無視します。
Excel のデータ分析ツール(分析ツールパック)の中にある フーリエ解析機能に実装されている FFTのアルゴリズムは、Cooley–Tukey型 FFTに分類されるものを用いているようですが、出力要素の順番が今回のFFTと異なることに注意してください。
前回の解説ではN=64に設定しました。そこで、ダミーデータ(64個のデータに7個のsin波を含む)のサンプリング周波数Fsを40Hzと仮定した場合の具体例を以下に示します。
・インデックス k=0: 0Hz(直流成分)。
・インデックス k=1~31: Fs/64=40/64=0.625Hzから10.375Hz。
・インデックス k=32: ナイキスト周波数 (Fs/2=20Hz)。
以下に得られた結果を図示します。ダミーデータの周波数は計算上は4.374Hzですが、ほぼ同じ位置にピークが現れていることが分かります。
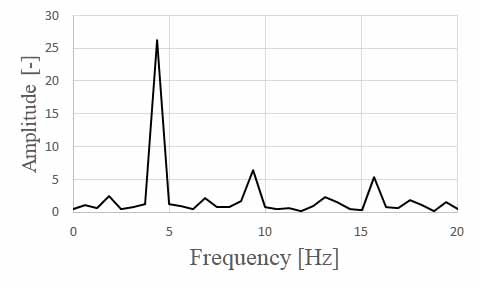
以下にダミーデータを64個のデータに10個のsin波を含む場合の結果を示します。ダミーデータの周波数は計算上は6.25Hzですが、ほぼ同じ位置にピークが現れていることが分かります。
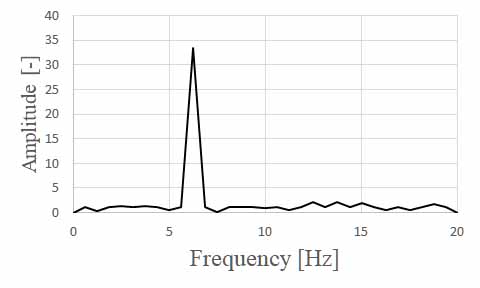
ダミーデータのsinの個数によりこのような差が生じる理由は、FFTの対称性と周波数分解能の関係にあります。
N=64 の FFT は分解能が 1/64なので、周波数軸は:0, 1/64, 2/64, …, 31/64, -32/64, -31/64, …, -1/64のようになりますが、周期性のため例えば正の k=5(5/64)は -59/64 と同じ周波数とみなされます。
FFT 出力が本来と異なる周波数にピークが発生する理由は、信号長N=64に周は非整数倍周期なので、波形が切れてスペクトルリークが発生するためです。つまり、信号長と周期数の関係では、FFTは入力がN点周期で繰り返されるとみなすため、整数周期でないと折り返し・位相回転・偽のピークが発生してしまうことになります。