今回はXBee3のMicroPythonで動作するFFTの実装について解説します。XBee3のCPUの型番は製品によって異なるもののArm Cortex-M4を使用しており、クロック周波数は約 32 MHz(外部通信プロトコル制御などで共用)です。また、RAM(動的メモリ)は約 32 KBであり、コード領域となるフラッシュは約 256 KBであり、厳しい制約条件があります。そこで今回は精度を犠牲にして簡易で軽いFFTとしてRadix-2 Decimation-In-Time (DIT) の反復型(iterative)FFTを用いることにしました。
FFTの原理的な説明は別の解説で示したいと考えており、今回はこのFFTの計算手順にについて簡単に説明します。このFFTは以下の手順で実行されます。
(1)ビット反転 (bit reversal):FFTのバタフライ演算を効率よく行うため、入力データをビット反転順に並び替えます。
(2)段階的なバタフライ演算(iterative loop):サイズ2, 4, 8, …, N=64 の部分配列ごとにバタフライ演算を繰り返し適用します。各段階で「twiddle factor(回転因子)」を計算し、入力データを合成します。
(3)回転因子の計算:e-j2πk/Nを cos_taylor と sin_taylor で近似します。
(4)最終的に自然順(0,1,2,…,63)で周波数成分が並んだFFT結果が得られます。
データ数をN=64として、ダミーとしてsin波を7周期含んだデータをサンプルデータ用いたRadix-2 Decimation-In-Time (DIT) の反復型(iterative)FFTのサンプルコードを以下に示します。 MicroPython Terminalでエンターを押してCtrl+Fで1^^^のプロンプトにしてから、マウスの右クリックでCopyを選択して貼り付けます。その後、Ctrl+Dでコンパイルして、スタートで自動実行に同意する「Y」を押して、Ctrl+Rで実行します。
import gc
# 円周率
PI = 3.141592653589793
# 複素数クラス:FFTでの複素数演算に使用
class Complex:
def __init__(self, real, imag=0.0):
self.real = real # 実部
self.imag = imag # 虚部
def add(self, other):
# 複素数の加算
return Complex(self.real + other.real, self.imag + other.imag)
def sub(self, other):
# 複素数の減算
return Complex(self.real - other.real, self.imag - other.imag)
def mul(self, other):
# 複素数の乗算
return Complex(
self.real * other.real - self.imag * other.imag,
self.real * other.imag + self.imag * other.real
)
def amplitude(self):
# 複素数の絶対値(振幅)
return (self.real**2 + self.imag**2)**0.5
def __str__(self):
# 複素数を文字列として表示
return "({:.6f}+{:.6f}j)".format(self.real, self.imag)
# サイン関数をテイラー展開で近似
def sin_taylor(x):
# -π〜πの範囲に正規化
while x > PI:
x -= 2*PI
while x < -PI:
x += 2*PI
x3 = x * x * x
x5 = x3 * x * x
return x - x3/6 + x5/120
# コサイン関数をテイラー展開で近似
def cos_taylor(x):
while x > PI:
x -= 2*PI
while x < -PI:
x += 2*PI
x2 = x * x
x4 = x2 * x2
return 1 - x2/2 + x4/24
# Radix-2 Decimation-In-Time の反復型FFT本体
def fft_iterative(x):
N = 64 # FFTサイズ
levels = 6 # N=64なのでlog2(64)=6段
# ---------------------------
# ビット反転でデータを並び替える
# ---------------------------
for i in range(N):
rev = 0
for j in range(levels):
if (i >> j) & 1:
rev |= 1 << (levels - 1 - j)
if i < rev:
x[i], x[rev] = x[rev], x[i]
# ---------------------------
# バタフライ演算を段階的に適用
# size=2,4,8,...,64まで繰り返す
# ---------------------------
size = 2
while size <= N:
halfsize = size // 2
angle_step = -2 * PI / size # 回転因子の角度の刻み
for i in range(0, N, size):
for j in range(halfsize):
angle = angle_step * j
# 回転因子(twiddle factor)を計算
tw = Complex(cos_taylor(angle), sin_taylor(angle))
u = x[i + j] # バタフライの上段
t = tw.mul(x[i + j + halfsize]) # バタフライの下段×回転因子
# バタフライ演算の結果を代入
x[i + j] = u.add(t)
x[i + j + halfsize] = u.sub(t)
size *= 2
return x
# ---------------------------
# テスト信号生成:周波数7のサイン波
# ---------------------------
samples_values = []
for t in range(64):
angle = 2 * PI * 7 * t / 64
samples_values.append(sin_taylor(angle))
# 複素数配列に変換(虚部0)
samples = [Complex(v, 0.0) for v in samples_values]
# FFTを実行
fft_result = fft_iterative(samples)
# ---------------------------
# FFT結果を表示
# ---------------------------
print("FFT結果(複素数):")
for z in fft_result:
print(z)
print("\nFFT結果(振幅):")
for z in fft_result:
print("{:.6f}".format(z.amplitude()))
# メモリ解放(ガベージコレクション)
del samples
del fft_result
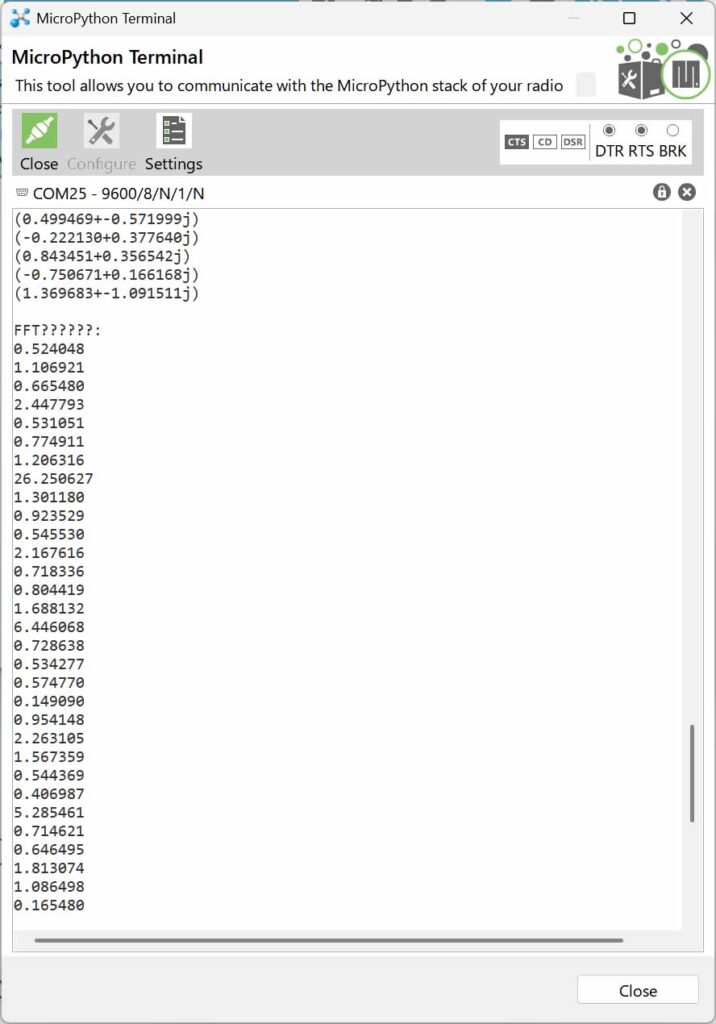
gc.collect()実行した結果を以下に示します。
実行すると以下のように結果が表示されます。
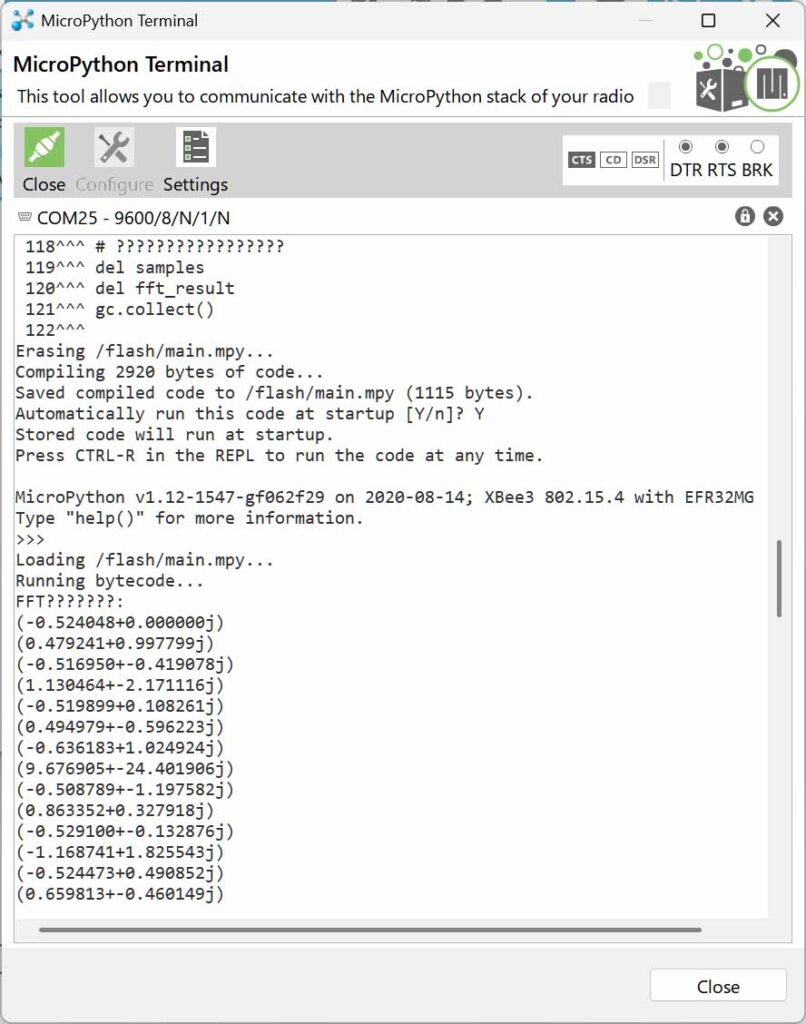
複素数から振幅を求めた結果を以下のように表示されます。Radix-2 Decimation-In-Time (DIT) の反復型(iterative)FFTにより振幅が得られていることが確認できます。この結果の解釈については次回に詳しく解説します。